Introduction

In classrooms across the nation, students are chewing their fingernails down the quick as they frown over their calculus homework. To them, the series of numbers and symbols on the page look like the headache-inducing language of an alien species, solving for X a nearly impossible task. In a fit of rage, they close their textbook and open a chat so they can bemoan the gratuitous torture that is math class with a friend.

“This is stupid! What’s the point, anyway? I’ll never use this stuff in real life!”

“I know right? There’s so much else we could be learning that’s way more useful!”

Wondering why anyone would ever go into a field that requires such nonsense, they push through the class dragging their feet and scratching their head nearly every step of the way. And when they’ve reached the minimum of what their secondary school or college admissions office requires, they’ll promptly strike math classes from their schedules and breathe a sigh of relief as they toss their folders full of formulas in the trash.

It’s a tale as old as the modern school system. And it’s something nearly everyone (but, perhaps, mathematicians and scientists) can relate to. But as such young people grow into tax-paying, mortgage-borrowing, retirement-fund-owning adults, they regret having not held onto those notes longer.

Pouring over a stack of complicated forms, receipts, and spreadsheets, the math never seems to add up right. The cruel classroom exercises have become real life, with much higher stakes: balance your budget and manage your finances or sink into poverty and bankruptcy. With confidence in calculating quickly waning, they realize they never thought would dawn and wish they paid a little more attention in calculus class.

Unfortunately, there’s no do-over. No time machine to take a quick trip back to that homework session years ago and tell their younger self to pay attention so they can understand the stock market later in life. And even if there was, do you think they’d listen?

With tiny powerful computers in our pockets, it’s hard to convince the younger crowd that taking copious calculus notes will be worth giving up a socialite Saturday afternoon. Heck, you, a distinguished grown adult, may not even be convinced yet.

Often, adults in the modern world don’t need to know much math, especially if they can afford an accountant. Most get by with only the barest knowledge of addition and subtraction (if that). We live in a world that has become quite anti-math, or rather, highly user-friendly for the un-mathematical person. Restaurants print tip calculations on the bottom of receipts, computerized registers and virtual payments have eliminated the need for counting change, and a quick Google search can answer questions about the Pythagorean Theorem or definite integrals. Nowadays, there are even apps for measuring the degree of an angle or which allow you to take a picture of a complicated equation and get an answer. But all this technology does is answer the procedural side of math. And, despite common misconception, the procedural part of math is not all of math.

Part of why students have such a hard time grasping and staying interested in math class is that they aren’t let into the secret behind the numbers. What your teacher never told you is that math class, just like all other required courses in school, is teaching you something much more valuable than the solutions to the problems on the pages of worksheets you’re given. It’s teaching you how to think better.

This is the idea of mathematical thinking, or in other words, the big-picture ideas and concepts behind calculus and trigonometry you were learning without even realizing it. Mathematical thinking isn’t math in the sense of learning multiplication and division, it’s the life lessons hidden between the formulas and theories. Whereas the math you learned in school was procedural, mathematical thinking is about the theoretical, conceptual, and—most importantly—practical parts of math.

Reading this book won’t make you a mathematician. Mathematical thinking is much more useful than that. It’s about learning how to implement processes to find answers, break tasks down into more manageable pieces, prove your points to make them more convincing, find and correct your mistakes more efficiently, ask the right questions and avoid assumptions, and better recognize and analyze patterns. Understanding these concepts will help to shape your thinking to become more logical, quantitative, and analytical. And that will be more valuable than any equation.

1

Why Learn Mathematical Thinking?

To say that equations are the heart and soul of math is like saying that a baker is someone with a lot of recipes. But a library full of cookbooks does not make a good chef. It’s only once someone has proven they can implement such recipes they are viewed as successful. From there, the more recipes they learn, the more of an authority they will be seen to be. Yet, no matter how many basic foods they make, they will only be considered a real expert once they’ve mastered the hardest dishes. Accomplishing these top-tier challenges shows they not only know how to repeat and memorize but that they understand the elements in a way that can be applied to other recipes and contexts.

Once you’ve mastered a baked Alaska, you can make almost any dessert. Because you haven’t just learned how to make a frivolous, over-the-top creation of cake and ice cream. In the process, you’ve learned the foundations of meringue making, cake baking, the finesse of frosting, and the precision of a blowtorch. Maybe, if you went all out, you’ve even learned how to churn a mean Neapolitan ice cream from scratch.

The recipe is just a formula, which can be written down, looked up, and followed when the rare occasion strikes that one needs a fanciful sweet. It’s a resource. Whereas the real value comes from the lessons learned by getting your hands dirty, cracking the eggs, and beating the batter. That hands-on practice is what makes you a better and more intuitive baker. After all, a recipe is only good for knowing how to make baked Alaska one particular way. If you wanted to spice it up or make something else, this step-by-step method won’t be very helpful. It’s the techniques you pick up along the way that will be transferable to other projects.

What is Mathematical Thinking?

Mathematical equations are like recipes. They’re tools for solving a problem, not solutions in and of themselves. To wield them effectively outside of the explicit context they were learned, we must also understand the skills and reasoning behind them. Mathematical thinking is where these ‘recipes’ find real-world context and usefulness, transferring those procedural elements into practical ways of doing and thinking. While the complicated calculus equations from high school can stay buried in a drawer for most of life with our baked Alaska recipe, the ability to think mathematically is something that can be used nearly daily to help solve a variety of issues.

Remember how you would spend lesson after lesson on equations in different contexts? And spend hours and hours on showing your work? How you would puzzle through tests where you had to figure out which equation was suitable where? And how you’d always wonder why they threw such curveball questions in that you never seemed to have practiced before? These problems weren’t there just to make things more difficult; they aimed to flex your mathematical thinking muscle.

While we were too busy moaning about the difficulty of math in high school, we didn’t realize that, beneath the numerals and symbols, these tests and tasks were teaching us how to interpret situations to apply the correct procedures and strategies, even if the issue was new to us. We were learning how to prove our answers and verify our accuracy. And we were learning how to be more analytical and methodical. In other words, we were learning how to problem-solve.

Despite what students may think, math was not created as a form of torture. People simply came up with equations to figure out real-world issues. It was about knowing how to get from point A to point B on a map and understanding how far apart the two were, about counting the coins in your pocket and knowing whether you had enough for the loaf of bread you were eyeing, and about noting how many hours had passed since you woke up that morning.

It wasn’t until around 500 BCE that math became the new thing. ¹ Rather than creating rules based on the routines and needs of life as the Babylonians and Egyptians had, the Greeks used math to prove things they couldn’t otherwise conceptualize, such as the powers of gravity. Suddenly, people were using concepts, previously employed for trade and taxation, to solve complex issues, like figuring out the height of pyramids, deciphering the area of circles, and even making sense of the stars. Equations became a way for great thinkers to explore ideas and theories they had about the world and test whether they were true. And that’s what math continues to be today.

Many may assume that we have the Greeks, and their schools of mathematics, to blame for making a big fuss out of math. But the truth is that it never went out of style. It has become even more popular.

The math we learn and teach today is largely based on concepts from only the last few hundred years. The subject has evolved from the measly concepts of addition, subtraction, multiplication, and division to what is now estimated to be between 60-70 categories, 50-60 of which have only emerged within the last 100 years. ²

People across the globe continue to get excited and devote their lives to researching the subject. More people today are interested in math than in its historical heyday. Some study concepts we’re familiar with, such as algebra and geometry, but many work with ideas beyond the everyday mathematician’s wildest dreams (or nightmares).

From studying and analyzing populations to planning cities, writing code, developing vaccines, deciphering weather patterns, keeping planes in the air, deciding whether you’ll win or lose at the slot machine, and so much more, math is all around us. As we’ve grown and evolved as a society, becoming more innovative and technological, math has grown and evolved too. Today, math is a ripe and limitless resource we can use as a tool to better explore and understand our world.

Math and the Abstract

In the 1980s, this sudden and large-scale change in how mathematics was viewed inspired the creation of a new definition. The subject became known as the “science of patterns” to better encapsulate its more abstract uses. ³ No longer was math utilitarian and functional, it was also interpretive and ideological. It wasn’t just about plugging in values to get an answer, it was about deeper understanding. It could be used to study the real or the unreal, the world as it was or as we imagined and perceived it.

Unfortunately, this new-age way of math was not communicated into the classroom. Or, more accurately, the ways for transforming the old methodologies and changing our perspective about what math could be were not clarified. Which is a shame. Because the wonderment and magic of math are in its ability to turn abstract and even intangible ideas into something that can be nailed down, calculated, analyzed, and studied.

Of course, math hasn’t changed. We merely changed how we see it and have gotten more creative with how we use it, but it has always been abstract. Even the basis of math is abstract, from numbers representing real-world objects and values to broader subjects like imaginary numbers that make no sense in a practical, real-world context.

As music becomes notes on paper and delicious food becomes recipes, practical real-world applications become abstract numerals and formulas. Perhaps, to the average Jill or Joe, math does not feel as delectable as these examples. But to many, math sings. They understand, more intuitively than most, that numbers and symbols are not what make math. They merely represent the action and thinking taking place. It’s the understanding that makes the magic. And when you know how to speak it, math can become a universal language for putting just about anything into a tangible form.

You may be thinking: “Isn’t knowing how to calculate fractions and add numbers together more useful for my life?”

The educational system would agree with you. With so much emphasis on practicality in school, there is no opportunity for abstract thinking. This has led to the idea that this way of perceiving math is more difficult. It can be, in the same way that painting a picture is harder than adding together denominations. The rules for how to do it aren’t as clearly defined, which is frightening. But it is also invigorating. The ability to quantify abstracts is what makes math so amazing…and useful in everyday life.

The Call for Abstract Thinking

In our modern world, the need for practical skills is waning. With powerful computers in our pockets and a world of technology at our fingertips, the average person rarely needs the functional aspects of math. Mostly, there are dedicated people and tools to help us with those tasks. We don’t need to understand how the airplane stays up to ride it from one place to another (or even to fly it ). And we don’t need to know how code functions on our favorite social media app to post selfies.

Meanwhile, the call for abstract thinkers, problem-solvers, and analyzers is growing. While you’ll be hard-pressed to find a job description that mentions trigonometry or algebra, most will have at least one of the words mentioned above. You’ll rarely need to have memorized an equation to solve a real-world issue but thinking outside the box and knowing how to strategize will be skills you use daily.

Ironically, as we see the need for math as we know it dwindle, we have unknowingly witnessed this rise in interest in mathematical thinking skills. Luckily, these facets of mathematics are much easier to call forth from memory than formulas from high school calculus. And I promise that, as we rework and strengthen this muscle in the coming chapters, there will be barely any calculations involved. Instead, we’ll look at the bigger picture of math and decipher all those life lessons we didn’t quite pick up on back in math class. And by doing so, we’ll make our thinking and approach to life a little bit better.

2

Precision

Math is a language. Just like any dialect, it allows us to shape ideas and abstract thoughts into a form that can be read and understood. Unlike other languages, however, it is universal, used in every country in the world. Although it is not spoken and looks much different on the page than what we understand as words, it has many of the same elements.

In math, equations comprise expressions, which are like phrases or incomplete sentences. These segments are part of a larger idea but lack a beginning or end. An expression could be just a number or variable or it could be a group of values and operations, such as 2 + 2 or (50 x 3) - 4.

Expressions can be short, containing only one or two numerals, or long, and can be combined to create larger ideas. However, they do not become a sentence until they are punctuated, usually with an equal sign, but sometimes with a less than, more than, or unequal sign. These two parts of a sentence, what we know of as the equation and answer, can also be thought of as an assumption and a conclusion. For example, 2+2 is an assumption while =4 is a verifiable conclusion of that expression.

Whereas in other languages a sentence can have many goals, the goal of a sentence in math is always to answer a question. Its purpose is to make a statement about the expressions, which comes down to whether it makes logical sense or not. To create a sentence, one must know, or prove, whether the theories posed in the expression(s) are true or false. If a sentence is proven true, it is considered closed.

The only way a sentence can exist without being true or false is if it is ‘open.’ Open sentences occur when variables are used or values are missing, for example, x + y = 8 or 4 + x > 10. These types of statements cannot be proven until x and/or y are known, thus, they cannot be proven true or untrue.

If a statement is not open, it must be provable to be true or false. But this can get messy in some uncertain instances. This is why math has so many rules in place for establishing what can be true or untrue.

Vacuous Truth and Conditional Statements

In English, we say that people are innocent until proven guilty. This is also true of math. If a sentence cannot be proven true, it is false. However, there is also a third option: “not guilty.”

One would think that “not guilty” would be the opposite of “guilty.” But it’s not. Rather, “Innocent” is considered the reverse. Innocent means that a person is considered to not have done the crime they are said to have been a part of. “Not guilty,” on the other hand, means that a person’s guilt or participation in the crime cannot be proven . Therefore, they have been let off the hook. But whether they were part of the crime or not can still be up for debate.

There is also a similar third option in math: vacuous truth. Vacuous truth occurs in conditional, or “if-then,” statements, which are often used to prove (or disprove) ideas. Vacuous truth refers to when either a condition is untrue (or inapplicable) or cannot be proven true. In other words, either the premise or a part of the “if-then” statement has no bearing.

For example, let’s take the phrase: “If dragons existed they would be pink.” Your first thought may be that this statement is untrue because it doesn’t say anything that is, necessarily, true. It is merely conjecturing. But it is vacuously true. Because dragons don’t exist, we can’t say what color they would be. Therefore, we can’t say they aren’t pink.

On the other hand, a conditional statement will be false if it cannot always be considered true. For example, if you said, “If it is morning, I am drinking coffee” and you drink coffee every morning without fail, this would be true. But if, one day, you don’t drink coffee in the morning, this statement becomes false, even though you usually drink coffee in the morning. There is no room for “sometimes” in mathematics. To say: “If it is morning, I might be drinking coffee,” is equivalent to saying nothing. You might be drinking coffee, or you may not. So, what’s the point of telling us if it gives us no usable information?

What you could say is that “If it is morning, I am either drinking coffee or I am not.” This would be true, although it still doesn’t tell us much. But if you added just a few more hints, it could tell us a lot. For example, “If it is morning, I am either drinking tea or coffee.” Now we know that, if we see it is the morning, we can count on you having one of the two drinks in your hand. We can also reasonably assume that you will not have both drinks; either you will drink coffee, or you will have tea.

The more complex an “if-then” statement becomes, the more difficult it is to prove true as all parts of the sentence must be true for the entire statement to also be true. For example, if you said, “If it is morning and the sun is shining, I am drinking coffee.” Now there are two stipulations for drinking coffee. If either is proven untrue, say it is a gloomy morning, the statement will be untrue. It does not matter that one part is verifiable, as they have become codependent ideas.

The Ambiguity of English

This strictness in math is undoubtedly part of what makes it so unappealing, as it takes much more work to create a meaningful sentence. But it’s also what makes it so successful and purposeful. There is no room for maybes or uncertainties; everything has an answer. Everything is true or false.

This black-and-white thinking may seem stiff compared to our language, where ideas are much more free-flowing. In English, there’s no need for statements to have such dramatic purpose, or to hold such weight. All an English sentence needs to be “true” is that it can be understood. But even that can sometimes be forgiven.

Although we have a plethora of rulebooks and conventions in place for our language, many more than in math, there’s still so much room for mistakes. How often have you run across a sentence or headline that looks something like this:

“One person dies every 36 seconds of cardiovascular disease (CDC, 2021).”

At first glance, this sentence doesn’t seem strange. It’s a format we’ve become used to. So many sources use it for shock value and to put things into perspective. But it’s wrong. A mathematician would see this for what it was, as a phrase suggesting one unfortunate person is out there dying of a heart attack every half minute only to resurrect and do it again and again. Poor guy!

We run into these issues everywhere in our language, but we don’t notice them. As long as the general intent is clear and most people can understand what we mean, the way we say and write things is up to our artistic interpretation. But whether that idea will be understood clearly by others is somewhat of a shot in the dark.

Imagine you’re on a road trip with a friend and ask them to navigate. As you exit the highway and enter a gridlock of busy city streets, you rely heavily on their directions. In a series of quick maneuvers, they suddenly yell: “Turn here!”

“Left?” you ask frantically.

“Right!”

Which way should you turn? Does right refer to the direction or the correctness of the statement? With someone honking desperately behind you and no time to double-check, you won’t know until you’ve found yourself wedged into a one-way street.

“Synonyms” and “Antonyms”

Technically your friend was right (i.e. correct), but they weren’t clear. They could have described what they were saying better, such as by saying “You’re right,” or “That’s right,” or they could have picked a more precise word. There are plenty of synonyms for this situation, such as “yes,” or “correct.”

Math has synonyms too; there are multiple ways to describe or show one idea. For example:

105+520/22+2+2+2+2

These expressions mean the same thing, yet you’d never use 2+2+2+2+2 if you could use 10, as you’d never say, “a habitable planet populated by homo sapiens” when you could just say “Earth.”

More so than in English, math is serious about brevity. The point of math is to shrink large concepts into much smaller ideas, i.e. symbols and numerals. Whereas in English, there are many words you can choose from to mean almost the same thing, math is resolute in that you should always choose the shortest way to say what you mean to say. Otherwise, your equations will take up pages and pages and be hard to read.

Math also has “antonyms” in a way. But, like its form of “synonyms,” they are much more resolute in their definition. While in English antonyms can be directly correlated or only subjectively related, a mathematical antonym, known as a negation, has to be a clear opposite. Because of the rules of sentences, this means that if a statement is true, its negation will be false and vice versa.

In English, the negation of something is not as obvious because there are so many interpretations of sentences and words. Take for instance this sentence:

“All memoirs are boring.”

Is the negation of this statement:

All memoirs are exciting.

All fantasy books are not exciting.

Not all memoirs are boring.

Some memoirs are exciting.

Since the original statement is false, the negation must be true. This means that option A can’t be the negation as it is false. Not all memoirs will be exciting. Option B can also be ruled out because it is not in direct opposition to the initial statement. Some may consider fantasy to be the opposite of memoirs, but it does not specifically correspond with memoirs. The statement was about memoirs so the negation must also be about memoirs. Otherwise, the sentences cannot be proven as related. Fantasy books being exciting says nothing about the content of memoirs. They’re separate issues.

Both options C and D could be negations. They are true and oppose the original statement as they disprove its standing. If some memoirs are exciting, not all of them can be boring.

In this example, you used your background knowledge of memoirs and fantasy books to establish what the sentences meant or didn’t mean to assert whether they were true. This is largely how English works. It is interpretive and based on our previous experiences and biases. This allows us to understand intent and express it in multiple ways while still being understood. But it leaves many gaps and inconsistencies that can lead to difficulties and misunderstandings.

When we see a statement such as 2 + 2 = 4 in math, we can prove that it is true and understand its context because the concept of each piece of the puzzle is defined. Our ideas of “2” and “4” are rigid and fixed. They leave no room for our emotions on the subject.

However, the word “memoir” comes with a host of different contexts and connotations depending on who you are. Everyone has a slightly different response to the phrase and, thus, will get a slightly different meaning from it. In most cases, these align closely enough between individuals that we can still communicate ideas effectively. But not so effectively that we always come to the same conclusions when those concepts are strung together into more complex ideas.

In English, context is everything, it makes up nearly all meaning. For example, “old” to a child means something different than it does to someone who has just had their 100th birthday. Likewise, the specific definition of “cold” to someone who lives in Alaska will differ greatly from someone who lives in Texas.

The Precision of Math

The beauty of the spoken and written word lies in their abstract nature open to interpretation. But the same trait that gives it this strength can also be its weakness. When we get sloppy, wordy, and inattentive to our language, it fails us. We end up with headlines that aren’t correct, navigators that aren’t helpful, and a host of other mistakes. Contrarily, the handful of rules that dictate how math is read and understood make it as concise, clear, and efficient as possible.

Although in casual speech we don’t need to be as strict with our wording as we do in mathematics, relying on every statement to be true or untrue, we could learn a lot from the core conventions of the language of mathematics. Above all, we might try to speak and write with a little more purpose and make sure we’re being as clear, succinct, and precise as we can be. If we did so, we might find our arguments and statements become more provable and able to stand up against those who would challenge them.

Errors in Reasoning

Making a mathematically sound, well-reasoned decision is not easy or simple. Common cognitive fallacies can trap and lead us into poorly reasoned decisions. By reviewing some of these fallacies, we can reduce the chances we’ll fall prey to them, or at the very least we’ll be able to recognize them promptly and respond appropriately.

Synonym Errors – This error occurs when one word is replaced with another, but the words do not have the same meaning.

Non Sequitur Errors – This error occurs when the argument does not follow logic. Essentially, the conclusion is not viable with the available facts.

Red Herring Errors – This error is an unrelated reference used to distract from the argument. The term red herring derives from the use of smoked and salted fish with a strong smell to distract hounds during English fox hunts.

Unsupported Generalization Errors – This error applies specific facts to a broad generalization with no justification.

Poisoning the Well Errors – This error simply means the argument is weakened due to criticism within the argument itself.

Cause and Effect Errors – This error sets up false choices between two choices while ignoring other possible options.

Begging the Question Errors – This error occurs with something that is believed to be true, but has not been verified, to support an argument.

Comparison Errors – This error looks for similarities or differences between two unrelated topics.

Questionable Authority Errors – This error occurs when using a source that is not an expert on a specific issue.

Contradiction Errors – This error states the opposite of what has been stated in the argument.

Inconsistency Errors - This is when parts of an argument are in direct opposition.

Omission Errors - This error occurs when a necessary piece of the argument has been left out.

Oversimplification Errors – This error reduces a complicated issue down to something simple.

Sampling Errors – This error relates to the data used to conclude. The sampling size may have been too small or there may have been an unreliable sample group ¹⁷ .

Ad Hominem Attack – This is an argument made on a person’s character or situation in life instead of the argument presented.

Card-Stacking – This error is based on only using facts that show the person positively making the argument.

Bandwagon Appeal – This is an attempt to conclude an argument right because ‘everyone else believes it.’

Argument to the People – This error tries to win people over by appealing to the emotions of others and creating a mob mentality in the heat of the moment instead of relying on the facts ¹⁸ .

Exercise

Keep a close eye on your newsfeed this week and look for ambiguous and imprecise wording. Is the sentence correct (in its spelling and grammar)? And is its wording clear? Look at what in these statements relies on your previous knowledge and what is defined. If you find unclear statements, think through how these could be made less ambiguous.

3

Specializing, Generalizing, Convincing, and Conjecturing

Despite what you may think, even the best mathematicians don’t always know the answer to an equation immediately. Just like an accomplished writer will occasionally stumble on a vocabulary word they are unfamiliar with or get tripped up by a comma splice or other grammatical error, those who are highly knowledgeable about the language of math won’t be able to get it right every time on the first try.

Like any skill, growing masterful at math is about practice, trial, and error. The more you mess up, the more you’ll learn and get better and the more likely you’ll be to get it right next time. This can be a frustrating and time-consuming process, as anyone who’s tried to master a skill will know, but it is worthwhile in the end.

When you make a mistake or fail, you’re not just knocking off another option and narrowing down the choices for a correct solution. You’re also putting your learning into practice by testing and using elements of the problem in new ways. The more you test yourself using examples, the more you will remember, solidify, understand, and connect with the solution and, more importantly, the process for finding the answer.

Specializing

Imagine heading into a store on Black Friday, clutching a stack of flyers, coupons, and a firm belief in sticking to your budget and not getting out of hand like last year. You head to the tech section, on the hunt to buy a new laptop that is originally $1,000 but is now 30% off. That’s straightforward enough. But you also must factor in taxes and fees, which are another 10%. You stare at the percentages, unsure of where to start. Should you calculate the tax first or the discount?

The only way to discover the solution is to open your calculator app and scribble down equations to see what works. First, you try to calculate the discount: $1000x0.30 is $300, so the laptop will be $700. Then the tax would be $700x0.10 or $70. $700+$70=$770 for the total cost.

That’s all well and good. But what about a tax-first approach? You know that 10% of $1,000 is $100 of tax, making the total price $1,100. Then, if you multiply that by 30% (0.30), you get $330. Subtract $330 from the total price of $1,100 and you get $770 again.

Wait a minute! They’re the same? You frown over the numbers, wondering if you’ve made a mistake or if it was a fluke. You double-check the math, then plug in another price to ensure you’ve done it correctly. You see a few other laptops for $800, $1,500, and $2,000. So, you take out a slip of paper and crunch the numbers.

Go ahead, try it. Test a few other examples and see what happens. Use the prices above or come up with your own. Once you’ve finished, you could try a few other, more difficult examples. Try a 35% discount or 15% tax. See if it still works out.

Whether you have a hard time wrapping your head around this calculation or think it’s a breeze, it’s good practice to get to know the overall concept and ensure that all your bases are covered and that your situation wasn’t just an exception. This will make you more confident about your answer, so you won’t have any doubt walking up to the register. But, most importantly, it will also help you to understand why and how the answer is true, which will lead to a greater and broader understanding.

Specializing, thus we can conclude is when we pick a particular example from a general idea (in our case, in what sequence to calculate taxes and discounts) and prove the idea with as many examples as possible.

Generalizing

Specializing, by testing different scenarios like the answers above, is how all the mathematical equations and formulas we now rely on came to be. Before being adopted, these theories began as well-educated guesses that were then tested repeatedly by their makers to assert that they held up. And for years since, we’ve been testing them still. Eventually, these ideas went through enough iterations they were accepted as true and became a rule or a generalization.

Generalizing is the process of taking distinct examples and turning them into universal learning that can be applied to more widespread situations. Often, this is done by breaking a situation down into its base parts and identifying what changes and what remains the same while replacing specific variables. This may sound complex, but in reality, it comes naturally in the process of logically thinking through a scenario. You’ve already come to a generalization with the Black Friday problem by concluding that it doesn’t matter whether tax or discounts are applied first. By taking the concept and making it broader using other examples, we made it a general rule rather than an answer to only one calculation, which you can now use for the rest of your life. And that’s a much more powerful piece of information.

Specializing and generalizing go hand in hand. Specializing proves generalization, and generalizations become the learning that allows us to specialize. When we generalize, we look at the patterns that lie beneath the specifics of our situation to find a deeper and more universal understanding. Meanwhile, specializing is our justification for why the generalization works. Without specializing, generalization can easily become just a guess or a bias, especially because patterns often emerge in math that only go so far or are misleading.

Conjecturing

Sometimes, even our best generalizations and tests cannot give us a surefire answer. Here, it must remain a conjecture or a best guess. A conjecture in math is like “not guilty until proven otherwise” in court. It seems right but may not be absolutely true. A conjecture may even have been proven in most cases using specialization, but because not all scenarios have been -or can be - tested, so it cannot be convincingly verified as always true . As aforementioned, because statements in math must be true or false (never maybe or sometimes true) conjecturing presents a gray area… at least until it is proven or contradicted (if ever).

A famous example of this is Goldbach’s conjecture, which states that every even number greater than two is the sum of two prime numbers. This seems plausible enough. But, because testing all even numbers to infinity would be next to impossible, we can’t prove that it’s always true. Although we’ve proven it often. ¹

There were likely many conjectures posed before Goldbach’s “correct” answer. Not all conjectures hold for a long time, some are disproven in only minutes, or immediately. In other words, conjecturing can also refer to a hypothesis or prediction that can then find an answer. In most cases, this guess won’t be right the first time. It’s usually more useful if it isn’t. If you stumbled upon a right answer the first time, likely, you won’t go back to see if other scenarios would disprove the conjecture. However, testing more than one scenario is essential to prove a conjecture is true. Without being able to prove your work, a solution is as good as no solution, because it isn’t verifiable.

Sometimes, using what knowledge you have to sense and make a best guess and then investigate whether it holds is often the best and only way to come to conclusions. Accept that your idea will likely be a failure the first time around and just dive in. By doing this, you’ll find an understanding that will help to find a solution or to at least guide the next attempt.

Convincing

Usually, it will be impossible to test all scenarios and outcomes efficiently. At some point, you will have to decide that you are “finished” or that you have proven your conjecture enough that you can say with confidence it is true. There will always be a grain of doubt. The important thing is not that every avenue has been explored but that you have enough evidence and have completed enough tests to prove your work to another person.

Often, once you’ve gone through a problem thoroughly, you will become too close to it to see the flaws. Especially if you’ve had a hard go of it, finding a solution that seems plausible after all that work will feel so good and be so tempting to accept that you won’t want to investigate much further. You may even subconsciously brush aside ideas that will contradict you as you won’t want to put in the effort to continue working through the problem. A fresh mind or a different perspective will see these issues for what they are and help to verify whether the idea holds up.

Once you’ve gone through all the effort of investigating and testing a hypothesis yourself, present it to someone you trust to be on your side. Someone who will be kind about it and help you to double-check your work’s validity. If they can’t find any issues, muster up the confidence to bring out the big guns and seek someone you know will have a very critical eye, a skeptic. ² This will force you to explain your thinking in as airtight a manner you can. Bringing in someone who will prod your conjecture for all its worth to see if it holds up can point out flaws in your analysis as your inquisitor is also more likely to ask you questions you or your friends wouldn’t pose.

This process is based on mathematical thinking but can be applied to almost any area of your life. An idea is created, tested, and written up. Then it is read by a critic who tries their best to (professionally) wreck the argument. If it holds nonetheless, all parties can move forward with confidence that the generalization can be applied. Maybe someone will come along one day and find an example of where it is not true… but that’s a problem for the future.

Take Note

The processes of conjecturing, specializing, generalizing, and convincing often come up in the teaching of John H. Mason, a firm believer in the powers of mathematical thinking. A retired professor Emeritus of Open University, Mason is known for his work teaching the practical parts of math in approachable ways through his numerous books and workshops.

Mason asserts that one of the most important parts of problem-solving is not getting things right but getting things wrong and noting every step of the process, even when and where you get stuck. ³ Write down your thoughts, your opinions, your frustrations, and your ideas (no matter how dumb they may seem). By doing so, you’ll have all the material you need for future convincing and generalizing, but also reflections that could help in other situations or which could even assist you in discovering more about your mental processes.

Not only is this a good idea for math, but life. When you come to a problem, write down your thoughts and opinions on the subject. Try to think about the problem in another context. If you were someone else, somewhere else, in some other time, what would this problem look like? What are the pros and cons? Try to use examples from your past or from other people to see whether solutions will hold up. And if they do, generalize this idea to become a rule or principle. This exercise will not only help you to define your problem, which can often be part of why the solution is so hard to find but help to sort through the ways it can be solved. Usually, as you write, you will arrive at the answer you were looking for.

Exercise

Try to use this four-step process to solve the problem below, following Mason’s advice to write down your thoughts on the process.

Connect the nine dots below using only four straight lines. The lines must connect and cannot be traced over.

Remember that your first guess, or conjecture, might not be correct, and show your work as you specialize, drawing out possible solutions. Consider the ideas and rules you come up with to guide your thinking until you find the right answer and how you would prove you’re correct if you presented your result to a friend (or foe). Reflect on what issues you ran into with your thinking that led you astray and what led you in the right direction.

If you’ve come upon this problem before, think back on how you solved it and what realizations had to come to the correct conclusion (and what biases had to be overcome). Think about how this changed your thinking for future problems.

4

Mathematical Thinking and Its Companions

Mathematical thinking involves many types of cognitive processes such as analyzing, synthetizing, and thinking critically about things.

Synthetic and Analytical Thinking

Analytical thinking is defined as having the ability to think in careful and perceptive ways to solve problems, analyze data, and remember and utilize information. Analytical thinking skills are, simply put, problem-solving skills. They are characteristics and abilities that allow you to approach problems in a logical, rational manner to sort out the best solutions. When we analyze something, we break that bigger thing into smaller, digestible pieces and one by one, assess -analyze- them.

When we break apart the different elements involved in a situation, it’s easy to lose sight of how these parts interact with one another and within the situation. This is how we end up in ‘analysis paralysis.’ When the interactions aren’t as visible, our insight is also reduced. The thinking tool we use to make sense of interactions and how things work together is synthesis.

Synthesis is more than simply putting something back together after you’ve taken it apart for an investigation. If analytical thinking helps us understand the different parts of a situation, then synthetic thinking allows us to understand how these parts work together. Another example of the differences between analytical and synthetic thinking is if analytical thinking helps break things down to their basic components, synthetic thinking allows to find patterns across those components. Essentially, analytical thinking will help you pinpoint the differences while systemic thinking allows you to pinpoint the similarities. It’s a type of specializing vs. generalizing. Both of these thinking patterns are needed to think mathematically.

Synthetic thinking is more challenging than analytical thinking because the interactions can be harder to track. Synthetic thinking is constantly fluid whereas analytical thinking is static. While both analytical and synthetic thinking will help you find patterns and commonalities, synthetic thinking finds these patterns, themes, and commonalities faster and easier because it is specifically looking for them while analytical thinking is looking for differences. Both analytical and synthetic thinking have their limitations and both types of thinking rely on the other.

As an example of synthetic thinking, let’s think about advertising in the automobile industry. An ongoing Dodge advertising campaign tries to sell trucks. For years, the company has identified trends in consumer information and preferences to develop products and marketing strategies. These ad campaigns have synthesized several themes based on demographics, lifestyle characteristics, and psychographics. The ads promote strong and tough engines and bodies, the fact that Dodge is ‘made in America’ and an American company, and even feature characteristics to appeal to families because the truck can morph into a ‘wagon’ with some button pushing and seat rearranging. All these parts are synthesized to persuade you to purchase a Dodge truck, no matter where you are in your life. But the individual synthesized parts were put through rigorous analysis first.

Systemic Thinking

This type of thinking is defined as an easy technique, used to understand complicated problems and situations. Systemic thinking allows us to manage several elements of a situation together rather than one at a time.

Systemic thinking, systems thinking, and systematic thinking are different. They all have their meaning. Systematic thinking is thinking methodically whereas systems thinking is thinking about how things interact with one another. Systemic thinking is a simple technique used to adopt a system-wide focus.

The basic idea behind systemic thinking is that everything interacts with their surroundings; everything affects and is affected. When approaching things from a systemic thinking mindset, we can no longer manage individual parts in isolation. We take the parts together and manage them cohesively. We manage both elements of the situation and how the parts interact with one another.

The systemic thinking process is a four-step process that follows.

List as many components as possible. This might include problems, solutions, opportunities, needs, desired outcomes, and ideas.

Group common components together, and then state what each group has that makes them similar. From the above list, problems and needs might go together in the same group, and desired outcomes, ideas, and opportunities could go together in the same group.

Find a repeating theme across group descriptions.

Your process should look like: Components -> Subthemes -> Common Theme. This process kicks up your insight in any situation and you might wonder why you haven’t done this sooner.

It’s difficult to recognize patterns and themes when you first encounter a challenging situation. However, with practice and as your skills develop, you should be able to recognize them more easily. The experience of working with systemic thinking is more than just knowledge and skills. It’s more familiarity with the patterns and themes that will give you the ability to recognize them. But because the ability to recognize given themes and patterns can become ingrained in your brain over time, you may recognize them on autopilot. This means you’re not comprehending what the pattern or theme means in a situation, you’re just engaging in behaviors by rote because that’s what you’re used to. The idea is to purposefully find and understand the repeating patterns and themes in any situation. This allows you to continually improve and develop better insight into mathematical thinking. ¹

Systemic thinking combines analytical and synthetic thinking. The process behind systemic thinking is to list as many components as you can think of and then to analyze and look for the similarities between them. This contrasts with analytical thinking where the process is to list only a handful of components, rank them, select only the most important one, and discard all the others.

Analyzing problems within the context of the systemic theory differs from analyzing problems elsewhere. Analytical thinking insists on working with only a few components to keep the list you’re working with manageable and to reduce the workload. Analytical thinking within the systemic thinking context requires us to list several components and provide the most accurate and representative pattern. For example, in systemic thinking, the first step is analytical thinking: List as many components as possible. The second step is synthetic thinking: Find the common themes and patterns across those components.

Critical Thinking

Critical thinking is the capacity to analyze facts, formulate and organize ideas, stand up for and defend opinions, compare items, draw conclusions, validate, or invalidate arguments, and problem solve. Critical thinking assumes there is logic involved in problem-solving and it can be figured out and reasoned through. When conjecturing, a good sense of critical thinking is key to research and proving your statements.

Critical thinking is not going to be appropriate in every situation or for every decision. Take the example of romance. Critical thinking and logic cannot help you determine who to date or who to marry. These are decisions made by your intuition and emotional reasoning. This stands true for personal taste, in general. I will likely never be able to explain why I love Howard Chandler Christy’s World War I recruitment posters for the United States. I’m sure it’s because I also like his other artwork and his ideal ‘Christy Girl.’ This isn’t something I had to learn to love. It was automatic. But without a doubt there are important decisions in life that have to be thought about and mulled over such as what college to attend, whether you should even attend college or if trade school is a better option, or should you take that job on the other side of the country.

Critical thinking is important because it allows us to acknowledge our emotions, but not be controlled by them. Emotions can mislead us into thinking we are making the right decision when we aren’t. Have you ever heard that most eyewitnesses to crimes are unreliable? That’s for many reasons. Sometimes it’s due to outside influence, not getting as good a look at the perpetrator as the witness thought, or just the trauma of witnessing a violent crime. But it is well known amongst criminal trial attorneys and prosecutors that an eyewitness is one of the least reliable forms of evidence, and that is why circumstantial or forensic evidence to back up that witness testimony is always needed to help prove a person’s guilt beyond a reasonable doubt.

Mathematical thinking differs from critical thinking in that the latter is more of an opinion-based approach whereas the former focuses on proving hypotheses and reaching a definite conclusion (true or false). When a person uses critical thinking skills the decision is made regardless of if the problem’s solution is true or false. Once critical thinkers are provided with information, he analyzes the information, interprets it, and then draws conclusions using what they know about the world. Critical thinkers then form their opinion on the topic being investigated. Mathematical thinkers take apart pieces of information. Each item is taken step by step to conjecture a generalized answer to the problem. They also use templates and formulas to prove or disprove this answer. ²

According to Dr. Roy van den Brink-Budgen, an expert in critical thinking, four traits are ingrained in critical thinkers: persistence, rigor, openness, and diligence ¹⁴ . In addition, Dr. Robert Ennis, Professor Emeritus at the University of Illinois, has also developed a list of skills that successful critical thinkers should be able to perform.

Judge the credibility of sources

Identify conclusions, reasons, and assumptions

Judge the quality of an argument—particularly its reasons, assumptions, and underlying evidence

Develop and defend a position on the issue

Ask the appropriate clarifying questions

Plan hypotheses or experiments, and assess experimental designs

Define terms in a way appropriate to the context

Be open-minded

Be well informed

Draw warranted conclusions, but with conclusions ³

These traits or skills can be taught or learned. Just like analytical thinking, critical thinking isn’t something you’re born with it’s a skill you acquire with education and practice.

A woman was near death from a special kind of cancer. There was one drug that the doctors thought might save her. It was a form of radium that a druggist in the same town had recently discovered. The drug was expensive to make, but the druggist was charging ten times what the drug cost him to produce. He paid $200 for the radium and charged $2,000 for a small dose of the drug.

The sick woman’s husband, Heinz, went to everyone he knew to borrow the money, but he could only get together about $1,000 which is half of what it cost. He told the druggist that his wife was dying and asked him to sell it cheaper or let him pay later. But the druggist said: “No, I discovered the drug and I’m going to make money from it.” So Heinz got desperate and broke into the man’s laboratory to steal the drug for his wife. Should Heinz have broken into the laboratory to steal the drug for his wife? Why or why not? ⁴

Some of the key questions you may want to ask yourself as you think about where you stand are…

Price gouging, which has been in the news quite recently specifically relating to ‘Big Pharma’ companies that have done this. There are the infamous Martin Shkreli and Valeant Pharmaceuticals scandals.

How do you feel about capitalism and free enterprise?

How much you value human life over other factors and, while you may feel bad for Heinz and his wife, that doesn’t entitle them to the drug or to steal another’s property.

These are just some questions to consider as you approach this dilemma. Remember, critical thinkers don’t worry about whether the issue is right or wrong.

Creative Thinking

Creative thinking is relating or producing a thing or idea not previously related. Creative thinking comes in handy when trying to solve problems when you’re panicked. Some might even prevent panic. When I took my two children to Disney World, they were young enough to enjoy the amusement park, but not old enough to reliably remember their parents’ names and phone numbers. I had temporary tattoos created for them with my name and phone number in case we were separated. Luckily, it never happened, but I got asked about where I’d gotten them from a lot of parents during our week-long vacation.

Mathematical thinking is logical whereas creative thinking requires your imagination and can lead to a literal fount of ideas and solutions. While each type of thinking is different, like all the other types of thinking in this chapter, creative thinking, and mathematical thinking are linked because they help one another. Mathematical thinkers often hit a roadblock; they feel stuck. To make progress, they follow creative leaps and bounds to conjecture a hypothesis that then they will try to prove. We will learn more about this connection in the next chapter.

Mathematical thinking is convergent. It breaks down to a few distinct ideas, answers, or solutions for further analysis and utility. In comparison, creative thinking is divergent, meaning it begins with a description and then splits in many directions to find many solutions.

Convergent features include logic, uniqueness, solutions, and vertical. Divergent features include imagination, multiple possibilities, solutions, and lateral. Mathematical thinking creates a tunnel vision to discover if a statement is true or false. Creative thinking requires a wide-ranging approach of all possible options, including those that, on the surface, appear to be unrelated.

Creative thinking is good for you. The creative process can improve your health in a multitude of ways. One is stress relief. ⁵ There are many creative activities you can do to help relieve stress in your life, and you can tailor them to your interests. Reducing your stress levels can help you prevent heart disease, Alzheimer’s disease, and depression. Creative thinking also increases and renews brain function, protects, and encourages neuron growth, which is vital in maintaining a healthy central nervous system. Creative activities can help in recovering after a major illness or injury or stress such as a breakup or divorce. This can include crafting, brain games, and even listening to music. ⁶

Recap

Analytical thinking is a cognitive process concerning four other concepts: synthetic, systemic, critical, and creative thinking.

Synthetic, systemic, critical, and creative thinking all work with analytical thinking (singularly or with another concept) to provide a wide range of options for approaching problems with analytical thinking.

Analytical thinking will help you find the differences in the components of a situation. The concepts will help you identify the similarities in the themes and patterns of the components.

Creative thinking is relating or producing a thing or idea not previously related.

5

Focus and Diffuse

When sitting down to write a book, I follow the same basic process: research, outline, write. Before bringing my thoughts to the table, I first ensure I understand the existing information and assess and create my own interpretations of it. From there comes the writing, which, if I’ve done my due diligence, will be straightforward enough, but not always easy.

When the going is good and I get into a state of flow or dive wholeheartedly into research, I turn on the metaphorical light switch in my brain, throwing it into a highly attentive state. Using this focused mode of thinking, I can dedicate myself to the task at hand, soaking in information like a sponge. Yet, despite my planning and research efforts, I sometimes still stare at a page and do not know what to write. My creative well runs dry and I come up against the dreaded writer’s block.

In these moments, I’ve learned that the best tactic is to close the document and walk away. This allows my mind a respite in which it can switch to resting-state networks, subconsciously working through the problem in the background of my mind as I go about other tasks. This resting, or diffused thinking, bounces the idea around in my mind until, at some point, as I brush my teeth, wash the dishes, or go for a walk, I stumble upon an “aha” moment and the path forward becomes clear. Everything clicks into place, and I rush back to my computer and turn on the switch in my mind that brings me back to focused mode.

We use focused and diffused thinking, often without realizing, for learning and getting better at almost everything in life. Whenever we focus and pour our attention into a topic, be it a lecture, a hobby, or solving a math problem, we turn on a flashlight in our mind, shining a pinpointed beam at the subject and blocking out all else in darkness. But eventually, we’ll get tired, or the lecture will be over, and we’ll need to step away and put the topic out of our minds. At least, we assume we put it out. But our brains continue to think about it, just in a different place and in a different way. We are switching the flashlight into a brighter, bigger beam that illuminates the path ahead with a diffused light. This allows us to see more, but everything is a little less clear. As we shine our light around, we might find something we want to investigate further and switch our flashlight back to focused mode to see it in more detail and go back to focused thinking. ¹ The process continues with this back and forth until we find what we’re looking for, i.e. the answer to our dilemma or a new understanding.

You’ve likely used focused and diffused thinking while reading this book. Unless you’re a voracious reader who has consumed this entire manuscript in one go (in which case, I’m flattered!), you’ll likely have taken a break here and there. In those intervals, did you notice yourself thinking back to one concept we’ve discussed? Perhaps as you went to check out your online shopping cart and saw the amount of tax you would pay. Or maybe it was at a more random time, such as when you folded the laundry or made lunch. Or maybe you didn’t think about it but, when you came back and read again, you found you seemed to have a better understanding somehow… without really trying. That’s the power of your diffuse thinking diligently working through your new knowledge!

The Einstellung Effect

When we run into issues when solving problems or getting into flow, such as writer’s block, the Einstellung effect is usually to blame. The Einstellung effect refers to preconceived ideas that hinder other, better solutions, creating mental roadblocks. ² For example, you may be set on including a particular idea or following a certain order of events in your book. When a different order might create a better story. The Einstellung effect keeps us set in our ways, makes our thinking brain inflexible. To get past this problem, it is necessary to clear away past preconceived notions or do further research (or, often, both).

Think back to the exercise in Chapter 3 with the grid of nine dots. Assuming the lines fit within the grid inevitably limited your solutions and stood in the way of you finding the correct answer, which relied on the lines extending beyond the dots. If you never accepted this out-of-the-box option, you’d never have gotten a correct answer. Yet it was a difficult assumption to overcome and unlearn.

In math class, the Einstellung effect often comes into play in a big way as we assume formulas and practice are the more important takeaways when this is like putting the cart before the horse. Instead of learning why and how these equations work, we simply use them until we have memorized them. In a way, this is like learning the grammar of a language before the vocabulary; we understand how it comes together but not what it means or when and why it’s useful.

This isn’t entirely our fault. Math classes are structured with an equation-first approach, with worksheets and workbooks filled with practice questions that undermine the bigger picture. General ideas become a sidebar of context for the problems, tricking students into thinking they are less important. Because the equations are what the education system wants you to walk away with (and what comes up on standardized tests) the broader understandings are viewed only as additional information, despite truly representing the key ingredients to the recipe. We will learn how to find the diameter of a circle or the hypotenuse of a triangle but not how to recognize where to apply that equation in real life.

Left-brain and Right-Brain

Because we’re taught math as a practice, or collection formulas, rather than overarching concepts and ways of thinking, we assume it is a “right-brain” skill. And it is. But it’s also creative and abstract in ways that require left-brain thinking. We understand that right-brain thinking is used for logical, analytical processes, associating it with subjects like math and science, while thinking of the left brain as a place for creative endeavors like art and writing. But this is an oversimplification.

We’ve largely disproven that people are left-brained or right-brained and the same goes for most skills. Mastering something usually takes a mix of technical know-how and creativity. We can learn to follow a recipe but making it our own is where the real expertise comes into play. Researching can serve us well until we need our artistic side to write the book. These activities use all parts of the brain. That’s what makes them fun… but also challenging; they stimulate different areas of our mind and abilities, although not always simultaneously.

As we’ve discussed in previous chapters, math is abstract. The idea that a group of people can be condensed into a numeral, that our worth can be summed up in simple figures, and that we can categorize intangible concepts like gravity with a few symbols, is about as abstract as it gets when you think about it. And putting those pieces together to come to new understandings, or to even create things like code, takes a lot of creativity.

We understand that taking a break is a necessity for creative endeavors, yet we think of math as something that can just be figured out if it’s stared at long enough. We assume that all the answers are out there, and we just need to find the right equation and insert the numbers in the right way, just as we did when we’d sift through our notes in math class to find the correct formulas for our homework. But there’s an art to putting together different mathematical concepts and theories to find solutions, a lot of out-of-the-box thinking, and a lot of time walking away and allowing diffuse mode thinking to take control.

The Benefits of Taking a Break

Focused and diffuse thinking can’t occur at the same time, just as you can’t have a flashlight on low and high-beam mode in tandem; one blocks the other from happening. But they do work in tandem to create understanding. First, you must learn an idea with focused thinking, i.e. by actively reading or participating in a lesson. Then, you digest that idea using diffuse thinking, allowing your mind to make connections between those ideas and your past experiences, other things you’ve read or seen, or within the material itself. Eventually, diffuse thinking can help spur or spark even more focused thinking, creating solutions that seem to appear out of the blue.

Therefore, diffuse thinking will only work if a focused, attentive effort has been put in first. You can’t understand a book unless you read it, play a symphony without learning the notes, or solve a math problem without knowing the scenario and skills to solve it. Diffuse thinking is not effortless; it’s a moment of respite between sprints in a race to the finish line.

We know that taking breaks with physical activity is necessary, but we forget that the same goes for our mental energy. We know that working out 24/7 won’t do us any good because our muscles must have time between sessions to recuperate to get stronger. We may do some stretching, foam rolling, or yoga to keep our bodies moving while letting our muscles do their thing. But pushing ourselves to the limit will only break us. Our bodies become drained quickly and give out, forcing us to quit.

The brain does the same thing. When we work on a task, a ticking time bomb of energy begins. Although we may not get shaky knees at the end, we may feel our frustration rise and our productivity plummet. Once that limit is reached, there’s no more we can achieve by working and staring at the problem. We’ll only be wasting time. We have to give our brains a rest. As we do, it will get stronger and build better connections and understandings, so that next time we come back to work, lifting those mental weights will get easier and easier.

But switching between diffuse and focused mode isn’t as easy as it seems. When you’re fighting to get through a manuscript with a looming deadline or a math problem on your homework, the last thing that seems helpful is walking away. It feels like giving up. Even if you do get up from your desk and walk around, shutting off focused thinking to allow diffused thinking takes a particular activity.

How to Switch Your Thinking

Both Salvador Dali and Thomas Edison knew the power of switching between thinking modes and did so often when stuck on problems by going to sleep. ³ Sleep is one of the best ways to turn on resting-state networks, as it forces the brain to shut off active thinking. In the REM stage (rapid eye movement) of sleep, our brains naturally interpret, analyze, and reflect on our day and create dreams by pulling together things we’ve experienced, learned, and thought about to conceive what appear to be strange fantasies. But we can harness and pinpoint this analysis to the problem at hand by thinking about the topic right before bed, ensuring it is the last thing on our subconscious mind as we drift off, preventing subliminal distractions.

If we always had to sleep to turn on diffuse mode, that would waste a lot of hours. It’s also possible to use diffuse mode on one subject while actively focusing on another to get the most out of your time. But it’s a fine line between putting a problem on the back burner and getting distracted. It can be easy to forget about a project when you allow yourself to do something else, creating a slippery slope to procrastination. Taking a break to watch one episode of a show can quickly turn into binging an entire season.

You can keep yourself on track by limiting distractions and ensuring breaks are short. In addition, the less brainpower you have to exert on the task, the better. Washing the dishes, going for a walk, folding laundry, taking a shower, having some lunch, or other more mundane tasks are best for diffuse thinking as they can be done on autopilot. This assures that no extra energy is expended that could be used for figuring out the problem. Plus, these tasks aren’t too time-consuming.

Chunking

Without realizing it, we often use our diffuse thinking to draw connections between separate pieces of information with similar meanings, a technique also known as “chunking.” This process is like taking learned information and sorting it into mental files so they can be recalled easier, later. For example, imagine you want to learn to draw and buy several books on the subject. Then, you sketch a figure. To do so, you won’t remember one piece of advice that came from one book and then remember another piece of advice from another book. You would think about the concept of “sketching” and memorable concepts from all sources would come to mind. You will get a general idea, or the gist, which is enough to apply it. By analyzing the material to sort it into chunks and creating these easier-to-memorize takeaways, your brain spends time with the material and views it at all angles until it finds a unique way of learning and understanding that will better last.

When you chunk, you are first given raw data. This is the research material, the class lecture, the book, or the mathematical equations. This information doesn’t make much sense at this stage because it is presented with the words and viewpoints of another person. You feel no connection to the material and have no practice with it. It’s like having the pieces to a puzzle without knowing what the result is; each section only gives a little slice of the overall idea.

Then, you focus on the key points. You highlight, write notes, or look at key elements of the material and memorize them for later use. However, beyond the understanding that it is important, there is still little to connect you to the ideas. This is like looking at the picture on the box of the puzzle; you see the goal but putting everything together to reach it is another issue altogether. You probably still understand what it means because you haven’t yet gone through the process. You may recite and quote lines from a book or spit out equations. But if someone asked you for the deeper meaning, you wouldn’t be able to explain it yourself.

Then, chunks are formed. Like putting puzzle pieces together to form an image, this ties the bits of information together to create a bigger picture. Unlike a puzzle, the way those pieces come together is (somewhat) up to you. You can use your past experiences to add to this “puzzle” to create a bigger, better chunk that encompasses more concepts and create understandings that are specifically meaningful to you. The better you understand the puzzle, the more you can make it your own.

We often chunk ideas subconsciously, but we can be more methodical and purposeful about it to be more efficient. To do this, the first step is to use focused thinking to get to know the raw information. Spill out your puzzle pieces on the table and look at them. Introduce yourself to these new ideas by giving them your full attention without distraction.

Next, try to look at the final puzzle image or the gist of the new information. What are the main takeaways and overarching ideas? What is the end goal? Allow diffuse thinking to kick in by walking away and doing something else to process all these pieces and make connections.

Depending on what you’re chunking, you can use one of two strategies: bottom-up or top-down. In bottom-up chunking, you use specialization or examples to reiterate understanding and practice ideas. In top-down chunking, you understand the big picture, or the final image, and work to see where and how all the pieces fit together.

The Importance of Recall

When we can Google an answer or have notes to answer our question, we create an “illusion of competence.” ⁴ Because the material is in front of us, we feel as if we know it. But, if we walk away, we’ll realize that we have retained little. Recalling material from memory is more effective for solid learning than repeated reading. However, simply memorizing the information doesn’t usually create the most thorough understanding.

In school, there is often an emphasis on focused mode thinking in rote memorization. When we can write out equations from memory or recite lines from a book, we appear that we understand them. But this is only step two in the process of chunking. It has created a trigger to recall information, but no connections. Often, when we memorize things, they come to mind without us even having to think about them. In some cases, like driving or typing, this is very efficient. But it also means we’re not using our mental capacity. It’s a knee-jerk reaction, not understanding.

Chunking relies heavily on creating our own, unique connections, which is why diffused thinking is such an important part of the process. This helps us to practice recalling so it sticks much better because it uses our methodology. Chunking allows for information to be remembered more easily but also ensures that the material becomes a part of your active memory. Coming up with new ways of looking at a topic creates a deeper learning experience.

When you first learn something, it should be repeated soon after to solidify the new information. For example, if you hear something in a lecture, you’ll want to think it over that night. Or, if you learn a new dance routine, go through the steps a few hours later. If you do it before bed, all the better, as your mind will use diffuse thinking as you sleep to process and cement them better in memory.

Sleeping on ideas is not a magic key to getting out of practicing or studying. Repetition and recall are equally important. The more you practice conjuring up an idea, the more your brain gets used to storing and recognizing that information, creating and wearing down mental pathways to make them more accessible. The easier it is to visit these ideas, the more time you’ll spend thinking about them, even if it’s only in small doses. With reiteration, you’ll need to practice less and less.

Exercise

How many errors do you see in this sentence: Their are four errrors in this sentance. ⁵

You probably said three. But if so, you were only looking at spelling and grammar. Look again. Think about it. Maybe walk away and come back. You’ll see the fourth soon enough.

When you’ve figured it out, try something bigger: take a concept you’re interested in learning but have trouble remembering or understanding. For example, an idea from this book, vocabulary of a language you’re learning, a dance move, a line of poetry, etc. Look at or practice this piece right before bed. Bonus points if you talk through the idea in your own words, whether it be out loud or in your head. Tomorrow, see how well you remember it compared to days when you didn’t practice before sleeping.

6

Linearity and Nonlinearity

We are primed to follow linear reasoning. We’re doing it every day. A simple example of linearity would be when we go into a supermarket being hungry. One sandwich sounds okay but buying three is a better plan. Each time we think something is good to have and having more of it is even better, we’re thinking in linear terms. Why is linear reasoning so popular when a short reflection shows its wrongness?

We fail to assess that everything in excess reaches saturation. In economics, there is a term for this phenomenon, diminishing marginal utility. This law states that “all else equal, as consumption increases, the marginal utility derived from each additional unit declines. Marginal utility is the incremental increase in utility that results from the consumption of one additional unit. The utility is an economic term used to represent satisfaction or happiness.” ¹ For example, the first sandwich will feel great when you introduce it to your famished body. But will the third (or even the second) give you equal satisfaction? Unlikely.

Two principles of linearity

Linearity obeys certain rules. If we have two or more inputs at a point in time, the final output will result from adding all the outputs. I would like to introduce you to the principle of additivity and homogeneity.

The additivity principle states we can add the output of two things together and the combined outcome will be the addition of the output of each item in isolation.

For example, if two oxen could each pull 300 lbs. of cargo on a cart in isolation, they could pull twice as much (600 lbs.) when combined on a much larger cart. In mathematical terms, the additivity principle looks like this: 300+300=600.

The homogeneity principle states that the linear output is always directly proportional to the input. If we put twice as much into something, we’ll get twice as much out. In numbers, the homogeneity principle looks like this: 1x=2, 2x=4, 3x=6, 4x=8, etc.

In real-life terms, if you paid $40 for a wine from which you expected a certain quality, the principle states that if you paid twice as much ($80) you would get a wine twice as good. (If wine quality would be objectively measurable.)

Linearity is simple enough to conceptualize – it is partially why it is a popular thinking pattern. But is it useful in everyday life? Let’s look at two examples.

Garden Gear

Let’s say you want to fertilize your garden and two fertilizers are meant to improve the quality of the soil. You buy them and use both simultaneously. In this case, the output or result will depend on whether the two fertilizers influence each other. If they do not affect each other, it will be the properties of each fertilizer in isolation that will determine the output, the quality of your garden’s soil. There would be a lack of interaction between the two fertilizers, thus the linear model can capture this event.

However, if the fertilizers affect each other, it will be the interaction between them. This interaction will determine the soil quality. The linear model fails as it relies upon the additivity principle that connotes an additive relationship. But in this situation, simple additivity is not the case.

The basic reasoning of the additivity principle is that we can add elements together without considering how they interact. The example of fertilizers proves how frail linearity is in real-world scenarios. But before jumping to conclusions, let’s test the homogeneity principle using an example.

Button Up

The principle of homogeneity assumes that scaling doesn’t matter. Is that so, though, in the case of real-world events? Let’s say you have a store where you import one million buttons a year to sell. Assuming that you succeed, and you can sell all of your buttons by the end of the year, you scale up the import to two million buttons a year. If everything would be scaled linearly, the linear model could capture this. But in the real-world chances are low that all the other variables (demand, import fees, shipping time, taxes, etc.) would scale according to the laws of linearity. Would your costs scale linearly? What about market saturation? If you can’t sell the two million buttons your revenue will not grow linearly.

The takeaway of these examples is that linearity can’t capture feedback. It fails to consider the effect actions have on their environment. Linearity also lacks the potential to show how the environment will respond to an action, not only in space but in time. In other words, how will past decisions and actions feedback to affect the present conditions?

Why do we bother with linear thinking then?

Linearity is intuitive. The static properties of tangible elements that linearity captures are easier for us to understand and quantify as opposed to the elusive world of interactions between elements and their behavior.

Linearity gets a few things right. For instance, the interactions between the simple dynamics of cause and effect happening in social and economic behavior.

Linear models are easy to understand. They exclude qualitative questions and analysis. They are well-suited to the strict quantitative methods of mathematics and the reductionist approach of science.

Let’s look at a mathematical example where linearity is helpful.

Dianne is trying to choose between two internet providers. The first plan with T-Mobile would cost $20 per month for a set amount of data with an additional 25 cents as cost per every additional MB (megabyte) she uses. Her second option, Verizon, is $40 per month, but their cost per additional MB is only 8 cents. Which should she choose?

By now we should feel intuitively that the choice will depend upon how many extra MB she expects to consume monthly.

Let’s write down the two equations for the cost in dollars in terms of the MBs used. The number of MBs is the independent variable; that will be the x. The cost depends on the MB. Thus the cost per month is the dependent variable, the y. Our equations will look like this:

For T-Mobile: y = 0.25x + 20

For Verizon: y = 0.08x + 40

Let’s write the equations in slope-intercept form (y = mx + b), and illustrate them as a graph:

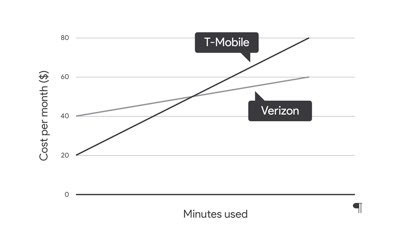
Picture: T-Mobile –Verizon Graph

The plan for T-Mobile has an intercept of 20 and a slope of 0.25. The Verizon plan has an intercept of 40 and a slope of 0.08. To help Dianne make an informed choice, we need to find where these two lines cross. Let’s solve the two equations.

Equation T-Mobile gives us an expression for y(0.25x + 20), so we can substitute this expression directly into equation Verizon:

0.25x+20=0.08x+40 subtract 20 from both sides

0.25x=0.08x+20 subtract 0.08x from both sides

0.17x=20 divide both sides by 0.17

x=117.65 MB

The number is not pretty but we can conclude that if Dianne uses an extra 117.65 MB a month, the two plans would cost the same. Now let’s go to our graph to assess which plan is better if she uses over 117.65 MB and which is better if she uses less. We can see that the T-Mobile plan costs more if she uses over 117.65 MB and the Verizon plan costs more if she uses less than 117.65 MB.

If Dianne uses 117.65 MB or less each month she should go for T-Mobile. If she estimates she’ll use 117.66 MB or more she should take Verizon’s plan. ²

Simple linear equations can be useful for minor everyday decisions.

We live in a nonlinear world.

In nonlinearity, “the output is not proportional to the change of the input.” Nonlinearity is an important part of mathematics and science with a special interest to engineers, biologists, physicists, and other fields of science nonlinear in nature. Nonlinearity sets out most real-world phenomena, yet it has been assigned the role as an alternative to scientific or mathematical analysis as opposed to linear thinking. Why?

Because, as we discussed above, linearity was and is easier to model. From a scientific viewpoint, we understand the world through our models. Setting up a model for two variables is easier than capturing all the influencing variables related to an event. It is almost impossible. Thus, even though our world is complex and operates by the laws of nonlinearity, scientists simplified their tools of understanding, so they at least have tools to use.

In the past centuries, the scientific focus has been grated largely to simple, linear interactions. These were organized into neat equations because they could be easily encoded in scientific language and understanding.

As the fields of mathematics and science developed, the models through which they examined the world also became more sophisticated. They offered a wider, more complex representation of reality. The current approach to nonlinearity is the byproduct of the past few decades. As our world expanded, sped up, and became undeniably interconnected, scientists saw and defined the new ways of thinking about nonlinearity. ³

The Swedish Conundrum

The linearity-nonlinearity-related thinking fiascos can’t only hijack our cell phone plans. Mixing the two can play out on much larger scales such as international politics, or national health assessment. Let’s see an example of both.

Jordan Ellenberg, the author of How Not To Be Wrong, shared the following story in his book. I find it too perfect not to share it with you. Our story begins when Mr. Daniel J. Mitchel of the Cato Institute published an article with the title, “Why is Obama Trying to Make America More Like Sweden when Swedes Try to Be Less Like Sweden?” ⁴ Fair question, you may think if you have no information on the subject. But with any bold claim, the one making it should provide some proof. And Mr. Mitchel did. Take a look at the picture below:

Picture 2: Extracted from How Not to Be Wrong, pg.22

When the Affordable Care Act was still hot news in the media, people such as Mr. Mitchel were questioning why Mr. Obama was trying to introduce costly welfare expenses when countries with the word as their middle name, such as Sweden, are trying to cut back on them. The picture above illustrates how the Cato Institute viewed this issue. The x axis represents prosperity, which peaks in the libertarian dream state. The y-axis shows that the more “Swedish” you are, the more your country is drowning in the red pit of socialism. So, Sweden, realizing where it was headed now tries to crawl leftward and up on the chart, while “ignorant” America is doing its best to go right and down to high five them. If this story would follow such a linearly explainable structure, this would be a fair representation.

But let’s examine how would nonlinear thinkers illustrate the same problem?

Picture 3: How Not to Be Wrong pg.23

This Bell curve gives us a different view of where maximal prosperity is. As we see, Sweden became a little too “Swedish” and, upon realizing that, introduced cuts in benefits they are now trying to impose. The US, however, is still not “Swedish” enough. To reach that sweet prosperity spot, they still need to help people out with state-directed support systems such as the Affordable Care Act. If we examine this image, we see that both the US implementing additional welfare measures and Sweden cutting back on them can be correct choices simultaneously. In economics, politics, and other complex and interrelated subjects, reality is rarely if ever linear, and rarely if ever exist in extremes. The truth is somewhere in the middle. “Nonlinear thinking means which way you should go depends on where you already are.” ⁵

“Will All Americans Become Overweight or Obese?” 

This question, again, seems thought-provoking in a society that deals with a lot of obesity-related health problems. But the article with the title above didn’t leave the reader to ponder the subject for too long as they supplied the answer, “yes, by 2048.” Here even the not so skeptical readers may have raised a brow. This article, just like the Cato Institute, missed the fact that not all lines are linear. Let’s see what went wrong.

To explain the obesity apocalypse, I want to introduce a concept used by social scientists called linear regression . It is “a model that assumes a linear relationship between the input variables (x) and the single output variable (y). More specifically, that (y) can be calculated from a linear combination of the input variables (x).” ⁶ To understand this seemingly complicated description, let’s go back to the question of overweight Americans. The National Health and Nutrition Examination Study, NHANES, tracks a variety of health-related information of a representative sample of Americans. They have been following the increasing trend of overweight in the US. (To clarify, when they talk about overweight, they refer to people having a body mass index of 25 or higher.) ⁷

At the beginning of 1970, about 50% of Americans were considered overweight. This number crawled up to almost 60% by the end of 1980. In the mid-2000s, almost 75% of Americans were deemed overweight. Youfa Wang and co., the authors of the article saying that all Americans will be overweight by 2048 probably used a false linear regression, which could be illustrated as such:

Picture 4: False linear regression

As you can see, the number of overweight people keeps increasing over time in a steady line and by 2048, it will hit 100%. If things would work like this in real life, by 2070 over 115% of Americans would have weight problems. The growing trend is not a straight line, despite how it may look at first sight. Instead, it looks more like this line:

Picture: The real line of overweight growth

The growth speed of the percentage of overweight people will slow down as it approaches 100%. Some people will never become overweight. They may be less in numbers, but some will stay fit. So at some point, the line will flatten below 100%. Bottom line, not all lines are straight. If the overweight percentage increased by 1% last year then the same will happen over the coming years. That’s what Wang et al. did, when they concluded that 100% of Americans will be overweight by 2048, they applied false linearity.

Avoid assuming that the rate of change of a quantity will remain constant. If the problem is linear then it will, but first, you need to prove your assumptions.

To avoid the trap of linear bias, know its existence. Educate yourself about what linearity is – this book is a good start. Simultaneously, read material and solve problems that involve nonlinearity. My book called The Systems Thinker – Dynamic Systems is a great primer for nonlinear phenomena, such as chaos theory. If you would like to delve deeper into the topic, read Steven H. Strogatz’s book Nonlinear Dynamics and Chaos.

7

Probability and Risk

Playing the lottery is a global phenomenon but do you know its origins? Back in the day when Italy wasn’t even Italy, just a collection of city-states, Genoa – one of the city-states – had a rather peculiar practice when seasonally electing its governatori . Every six months, in the Petty Council, the 120 members would write their names on a piece of paper, and two would be drawn by chance to fulfill the governor position. Soon the city gamblers would make bets on the elections. As time passed, these bets were worth more money. Eventually, the gamblers realized that they don’t need an election to bet on pieces of paper. Before long, Genoa ran its lottery system with people betting on five numbers – the more correct guesses, the higher the prize. ¹

This isn’t too far away from our lottery system today. Thanks to the Genovese gamblers, from Shanghai to Paris, from Moscow to Cape Town, the presence of lotteries is pervasive. “Stupidity tax” as some may call it. There is something very attractive about winning millions of dollars for the purchase of a single ticket. But let’s see how mathematically sound playing on the lottery is.

Lottery, and gambling, are a mixture of probability and risk. The less probable something is, the higher the risk you will lose, but the reward is also higher – which is why so many people engage in this guilty little pleasure. Lottery tickets are fairly cheap, this further increases their appeal. And if you buy two tickets, oh my, you doubled your chances to win those millions. Or have you?

How would a simply-structured lottery game look in the realm of mathematics? Let’s say, there are 10 million combinations, and the grand prize is $7 million. Assuming that a ticket costs $1, you would need to spend $10 million to win for certain. But if you did that, you’d be $3 million short, even if you won the jackpot. That’s not a great strategy. If you bought one ticket, you’d have a one-in-ten-million chance. What if you got two tickets? Sorry, it doesn’t become one-in-five-million, as many people think when they say they doubled their chances with a second ticket. In this case, your odds are two-in-ten-million. In 9,999,998 cases you’ll still lose. But hey, your odds are improving. Your chances to break even will require a $7 million investment. When you have those many tickets, your chances to lose shrunk to “only” 30%. But buy one more ticket, and you’ll become a guaranteed loser. Why? Because it means you paid $7,000,001 and the maximum you can win is $7 million. $1 or $7,000,001, you’ll lose either way. ²

Expected Value

One mistake we often make is confusing probability and risk. We use probability to gauge how risky a bet or an investment is, and we assume that’s all there is to it – wrong. For instance, if we played roulette in Vegas, we could calculate the probability of winning vs. losing money eventually by checking our expected value . The roulette wheel has 37 numbers, 0 to 36. Half are red, half are black. 0 is green and you can’t bet on it. If we bet $1 on black, because there are 18 black slots, our chances to double our money is 18/37. One would think that our chances to lose our buck is also 18/37. But let’s not forget about the green slot – so our actual chance of losing is 19/37. Knowing these numbers, our expected value is 1(8/37 x 1) (we win) - (19/37 x 1) (we lose) = -$0.027. ³

Eventually, in the long run, the house always wins. Why even play then? Because the expected value is more than just probability or risk. In the lottery example, the lottery tickets value is what it is, but its expected value is either $7 million or zero. Let’s check another example to understand the expected value better.

This summer I went to the Orange County Fair. The highlight of this fair, arguably, was its afternoon pig race. After the incessant nagging of my buddy whose pig, Hammy, “competed,” I agreed to bet $100 on the athletic swine. To simplify math, let’s assume there were 10 competing pigs, and my reward if Hammy won would have been $1000. If Hammy had a 10% chance of winning, my expected value equation would look like this:

(10% x $1000) + (90% x 0) = $100

However, $100 is not even a realistic outcome for my bet – as the prize is $1000. And most definitely is not what I would expect to happen. This equation would sound better if I considered it just as showing what would happen if I put this bet on many other pigs. Say, I would purchase 100 pieces of $100 tickets on, and I won say… 10 of them. Then my winning would amount to $10,000. I came out even, averaging $100/ticket. But what if the ticket’s price was $110? With the prize still being $1,000, I would lose in the long run. If the ticket’s price was $90, with a jackpot of $1,000, I would win long-term.

Finding the expected value of a bet, therefore, is critical to gauge your winning chances long term.

Car Insurance

Do you have car insurance? Most people in the US do. One of my friends, let’s call him Paul, is a salesman in Geico. (I have no affiliation with them. I don’t even use them. Sorry, Paul.) He sells 6-month policies, meaning for a single payment the buyer gets repair coverage for the next half a year. To not have an easy time following the numbers, I changed the rate to:

• Let’s say damage happens in $7,500 increments and can go up to $30,000 for a destroyed car.

• Let’s pretend that everyone who buys Geico’s policy (“the insured”) do so on the same day.

• The policy premiums (the sum the insured are charged with) are the same for everyone.

How can Geico determine how much to charge in premiums? Well, they need to predict how much money they will need to pay out in claims to the insured in the 6-month policy period. Let’s see how this would look like in the language of math:

Premium = expected claims amount per each insured = expected accidents (frequency) x expected dollars paid on each accident (severity). ⁴

Both frequency and severity are what we call random variables. These variables can have unspecified values, which lie on an “underlying probability distribution. A probability distribution describes the probability associated with each potential value of a random variable.” ⁵ So, for Geico to calculate the premium, they need to calculate the expected claims (E # of claims) of each driver over the policy period and how much each claim will cost (E amount of a claim). The premium thus can be written down as:

Premium = E(# of claims) x E (amount of claims)

Insurance companies calculate the actual distribution for the number of claims per insured per policy period based on historical data. To make our lives easier, let’s assume this is the probability percentage for claim frequency:

Number of Claims - Probability

0 50%

1 30%

2 10%

3 10%

Based on this information, the expected value of the number of claims would be:

E(# of claims) = Prob(# of claims = 0) x 0 + Prob(# of claims = 1) x 1 + Prob(# of claims = 2) x 2 + Prob(# of claims = 3) x 3 = (50% x 0) + (30% x 1) + (10% x 2) + (10% x 3) = (0/100)+ (30/100) + (20/100) + (30/100) = 80/100 or 0.80.

Now let’s create a similar chart for severity, a.k.a. how much will each claim cost:

Cost of Claims -Probability

$7,500 15%

$15,000 35%

$22,500 40%

$30,000 10%

Based on this chart we can conclude that most claim payouts, 80%, will happen in the mid-range. The expected value of the cost of claims will be:

E(amount of claim) = Prob(amount of claim = $7,500) x $7,500 + Prob(amount of claim = $15,000) x $15,000 + Prob(amount of claim = $22,500) x $22,500 + Prob(amount of claim = $30,000) x $30,000 = (15% x $7,500) + (35% x $15,000) + (40% x $22,500) + (10% x $30,000) = $1,125+$5,250+$9,000+$3,000= $18,375.

We have both random variables, so let’s calculate the premium using the formula we established above:

Premium = E(# of claims) x E(amount of claim)

= 0.80 x $18,375 = $14,700.

Ouch, pricey! These numbers are made up. No one would buy auto insurance at this price; they could buy a new car every 6 months for that! But you get the gist.

For the sake of practicing, try to do the following exercise on your own.

The next year’s premium:

Based on the data Geico gathered this year, they are recalculating their premiums. In 2021, this was the probability distribution of the number of accidents and how much claim was paid for each:

Number of Claims - Probability

0 40%

1 20%

2 15%

3 10%

4 5%

Cost of Claims - Probability

$7,500 20%

$15,000 40%

$22,500 25%

$30,000 15%

Recalculate the company’s premium for 2022!

8

Test Your Mathematical Might

Repetition and recalling are powerful learning tools. Tests utilize both to deepen your knowledge. I know, most of you detest being put on the spot and think that tests only make your life miserable. Think again.

When you’re under pressure, your mind concentrates on a new level. Try to remember how much material you retain after an hour of rigorous study. Now, how well do you remember the questions and your answers on a test? If you’re like most people, you will recall and retain much more information from the test. I can still recall that at my high school history finals, I’ve been asked why the Ottoman Empire couldn’t conquer Vienna in the 1600s. I happened to revise this information the night before (sheer luck), so I wowed my teachers by stating that Vienna was outside of the action radius of the Ottoman army. They could replenish food and military resources fast enough to overthrow the not ignorable Habsburg forces. I will never forget what action radius is because it has been reinforced in a testing environment. I don’t remember anything else from the night before the test I spent studying.

So, if you hate tests, I’m here to challenge your sentiments. My goal is not to turn you into a test junkie but to share tips that could benefit and push you to get through the ordeal with more ease thus making this invaluable practice more attractive.

How to deal with test anxiety?

Let’s tackle this question first. So many people dread tests because when the time comes to prove their knowledge, their mind goes blank. They knew the material before and will know after. But on the spot, they freeze. Does this describe you at all? If so, try the following approach.

Reframe what your test anxiety means. Anxiety provokes the release of a body chemical called cortisol. When your body gets flooded with it, you will hear your heart pounding, your hands may be sweating, and you may tell yourself that you’re terrified of this test. Stop right there. What if you rephrased in your mind what this test means? What if you thought about it as becoming anxious to do your best? ¹ This refraining can help you a lot in getting your mental power back.

If you are still anxious, notice the stories you tell yourself regarding your test. Do you have any attached secondary thought to it? For example, does “I’m terrified of this test” continue with “because if I don’t do well, my chances to become a doctor will be forever gone.” Is this second part true? Question the stories you tell yourself. Reframe your thinking. This is a mindfulness practice, a helpful one of that. You don’t need to buy into your fear-mongering thoughts. You can just observe them and let them go.

Take a few deep belly breaths, follow your inhalation and exhalation. This way you will send more oxygen to critical parts of your brain. Deep breathing also activates the parasympathetic nervous system, which is your calm and safe center. It’s beneficial if you practice deep breathing weeks before your big test so you get into the habit of doing it. Calming yourself will come more naturally if you don’t try this practice only on the spot.

The setting where you take your test is different than where you study or take practice tests. It’s helpful to you if you sneak in a class or lecture with a bigger headcount and try taking your drills there. That environment is more like the one where you will take the test. Sitting in your pajamas at home while watching a TV show will feel like being put on the spot.

Hard things first

I remember, when I was a student, my math tests were set up as follows: a couple of easy-to-tackle problems that had an almost obvious answer. Then some mid-weight contenders I could navigate with an additional 25% of brainpower. And then came these long, monstrous geometry calculations of ten attached concave triangles that were shapeshifting in front of my anxious mind.

Tests have this sequence because they are built on the assumption you will feel more confident about the harder problems if you can solve the easier ones with no trouble. And that’s true for some. But most people could benefit more from summoning the thought-shifting magic of their mind’s diffused mode. To access diffused thinking, focus on a problem for a period, and then go do something else. When you arrived at the last problem of a test that seems more complicated than rocket science, you won’t be able to focus on anything else.

What should you do then? Barbara Oakley, a professor of engineering, and leading mathematician suggests you start with the hardest problem first but quickly shift to easier ones afterward. ² She recommends scanning through the entire test once it is handed to you, looking for the most difficult problem. Once you identify it, solve it but unless you are making good progress on it, abort the mission after 2-3 minutes. Don’t get stuck. Work on the easier tasks and allow your diffuse thinking to kick in. Because it will kick in. By spending only a few minutes focusing on the most difficult problem, you “uploaded” it in your conscious awareness.

After you solved a few easy problems, go to the second most difficult task and spend a few minutes on that. Jump back to the easy tasks. Then revisit the most challenging, first problem. See if you got a new perspective, new ideas about how to solve it. Whenever you feel stuck or unsettled, go back to the easier tasks. Slowly you will make progress on the harder tasks, and you’ll be surprised by the ideas that come to you after a period of “rest.”

This test-taking strategy is great because you will make some progress with every problem and won’t feel overwhelmed if you encounter the hardest one last minute. You will also benefit from reducing the Einstellung effect, getting stuck on a particular idea for a solution. The only difficulty with this approach is that you need to “walk away” from the difficult problem for a time. Persistence is misplaced for challenging math tasks.

Try this on multiple-choice guess tests

What’s the most natural thing to do when you’re faced with one question and four answers? To read through the question quickly and immediately jump to the selection of the answers and see which could be the right one. Often the question is packed in a tricky way. There may be a hidden negation in it and then immediately, the answer is not the obvious one.

Before you even read the question, cover the answers. Then read the question, savoring every word. What does the question mean? Try to answer it. Then reveal the four guess answers and check if your answer matches any of them.

Key thoughts about tests

1. Insufficient sleep can deteriorate your ability to recall information. Have a good, 8 hours sleep the night before your test.

2. Consider tests as your ally for learning. They are necessary parts of your success story. Take them seriously but not anxiously.

3. Start a test by identifying and then reflecting on the hardest problem first. Then jump to easier tasks. Then go back to the hard one.

4. Be aware of how you think about tests and what stories you tell yourself about their importance and consequence. Reframe your negative thoughts. Breathe.

5. Double check your answers even when you think what you wrote is correct. Sometimes, when the Einstellung effect is active, you may have anchored on a solution. After spending some time apart, check if that answer still makes sense.

6. Walk away from this book right now. Spend a minute to recall what you learned in this chapter. Tell it to someone or just say it out loud.

References

Brownlee, J. (2020, August 15).  Linear Regression for Machine Learning . Machine Learning Mastery. Retrieved December 15, 2021, from https://machinelearningmastery.com/linear-regression-for-machine-learning/

Dash, Mike. Critical Thinking. (2012) What it is. How it works. Why it matters. Macat. https://static1.squarespace.com/static/59b7cd299f74569a3aaf0496/t/5afeb67003ce6445740c9563/1526642291284/CT_ebook_Feb_18.pdf

CDC. (2021, September 27). Heart disease facts . Centers for Disease Control and Prevention. https://www.cdc.gov/heartdisease/facts.htm

Devlin, K. (2012).  Introduction to Mathematical Thinking . Keith Devlin.

Example extracted from: Algebra 1. Solving Real-World Problems Using Linear Systems. Algebra 1. 2019. https://students.ga.desire2learn.com/d2l/lor/viewer/viewFile.d2lfile/1798/12632/Algebra_ReasoningWithEquationsandInequalities12.html

Goeke, N. (2021, July 12).  How Not To Be Wrong Summary . Four Minute Books. Retrieved December 15, 2021, from https://fourminutebooks.com/how-not-to-be-wrong-summary/

How to build your first GPS . (n.d.). Systemic Thinking. Retrieved December 15, 2021, from http://systemicthinking.com/strategy-fractals/gps/building-a-gps.html

Kenton, W. (2021, July 17).  Law Of Diminishing Marginal Utility Definition . Investopedia. Retrieved December 15, 2021, from https://www.investopedia.com/terms/l/lawofdiminishingutility.asp

Mason, J., Burton, L., & Stacey, K. (2010).  Thinking Mathematically  (2nd ed.). Pearson.

Mathematics of Risk . (n.d.). Westfield MA. Retrieved December 15, 2021, from https://www.westfield.ma.edu/math/MathWeb/Actuarial/PDFs/342-Intro-to-Risk.pdf

Nunez, K. (2016, July 20).  5 Proven Ways Creativity Is Good for Your Health . Verily. Retrieved December 15, 2021, from https://verilymag.com/2016/01/mental-emotional-health-creativity-happiness

Oakley, PhD, B. (2014).  A Mind for Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) (Illustrated ed.). TarcherPerigee.

O’Brien, J., & Audio, P. (2020).  How Not to Be Wrong: The Art of Changing Your Mind . Penguin Audio.

Rutherford, A. (2020).  The Systems Thinker – Dynamic Systems: Make Better Decisions and Find Lasting Solutions Using Scientific Analysis. (The Systems Thinker Series Book 5)  (2nd ed.). ARB Publications.

Udemy Editor. (2014, June 2).  Analytical Thinking: Why You Need It and How to Get Better . Udemy Blog. Retrieved December 15, 2021, from https://blog.udemy.com/analytical-thinking/

Wang, Y., Beydoun, M., Caballero, B., & Kumanyika, S. (2008, July 24).  NCBI - WWW Error Blocked Diagnostic . National Library of Medicine. Retrieved December 15, 2021, from https://pubmed.ncbi.nlm.nih.gov/18719634/

Watanabe-Crockett, L. (2017).  Critical Thinking . Wabisabi Learning. Retrieved December 15, 2021, from https://www.wabisabilearning.com/blog/critical-thinking-exercises-blow-students-minds

Notes

1. Why Learn Mathematical Thinking?

1 Devlin, K. (2012).  Introduction to Mathematical Thinking . Keith Devlin.

2 Devlin, K. (2012).  Introduction to Mathematical Thinking . Keith Devlin.

3 Devlin, K. (2012).  Introduction to Mathematical Thinking . Keith Devlin.

3. Specializing, Generalizing, Convincing, and Conjecturing

1 (Mason, J., Burton, L., & Stacey, K. (2010).  Thinking Mathematically  (2nd ed.). Pearson. p.14).

2 Mason, J., Burton, L., & Stacey, K. (2010).  Thinking Mathematically  (2nd ed.). Pearson.

p. 88).

3 (Mason, J., Burton, L., & Stacey, K. (2010).  Thinking Mathematically  (2nd ed.). Pearson.

p. 10-11).

4. Mathematical Thinking and Its Companions

1 Udemy Editor. (2014, June 2). Analytical Thinking: Why You Need It and How to Get Better. Udemy Blog. Retrieved December 15, 2021, from https://blog.udemy.com/analytical-thinking/

2 Systemic Thinking. (2018) How to build a GPS? Systemic Thinking. http://systemicthinking.com/strategy-fractals/gps/building-a-gps.html

3 Dash, Mike. Critical Thinking. (2012) What it is. How it works. Why it matters. Macat. https://static1.squarespace.com/static/59b7cd299f74569a3aaf0496/t/5afeb67003ce6445740c9563/1526642291284/CT_ebook_Feb_18.pdf

4 Watanabe-Crockett, L. (2017). Critical Thinking. Wabisabi Learning. Retrieved December 15, 2021, from https://www.wabisabilearning.com/blog/critical-thinking-exercises-blow-students-minds

5 Nunez, K. (2016, July 20). 5 Proven Ways Creativity Is Good for Your Health. Verily. Retrieved December 15, 2021, from https://verilymag.com/2016/01/mental-emotional-health-creativity-happiness

6 Nunez, K. (2016, July 20). 5 Proven Ways Creativity Is Good for Your Health. Verily. Retrieved December 15, 2021, from https://verilymag.com/2016/01/mental-emotional-health-creativity-happiness

5. Focus and Diffuse

1 Oakley, PhD, B. (2014). A Mind for Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) (Illustrated ed.). TarcherPerigee. p. 18.

2 (Oakley, PhD, B. (2014). A Mind for Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) (Illustrated ed.). TarcherPerigee. p. 17.

3 Oakley, PhD, B. (2014). A Mind for Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) (Illustrated ed.). TarcherPerigee. p. 32.

4 Oakley, PhD, B. (2014). A Mind for Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) (Illustrated ed.). TarcherPerigee. p. 61.

5 Oakley, PhD, B. (2014). A Mind for Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) (Illustrated ed.). TarcherPerigee.

6. Linearity and Nonlinearity

1 Kenton, W. (2021, July 17). Law Of Diminishing Marginal Utility Definition. Investopedia. Retrieved December 15, 2021, from https://www.investopedia.com/terms/l/lawofdiminishingutility.asp

2 Example extracted from: Algebra 1. Solving Real-World Problems Using Linear Systems. Algebra 1. 2019. https://students.ga.desire2learn.com/d2l/lor/viewer/viewFile.d2lfile/1798/12632/Algebra_ReasoningWithEquationsandInequalities12.html

3 Rutherford, A. (2020). The Systems Thinker – Dynamic Systems: Make Better Decisions and Find Lasting Solutions Using Scientific Analysis. (The Systems Thinker Series Book 5) (2nd ed.). ARB Publications.

4 O’Brien, J., & Audio, P. (2020). How Not to Be Wrong: The Art of Changing Your Mind. Penguin Audio.

5 O’Brien, J., & Audio, P. (2020). How Not to Be Wrong: The Art of Changing Your Mind. Penguin Audio.

6 Brownlee, J. (2020, August 15). Linear Regression for Machine Learning. Machine Learning Mastery. Retrieved December 15, 2021, from https://machinelearningmastery.com/linear-regression-for-machine-learning/

7 O’Brien, J., & Audio, P. (2020). How Not to Be Wrong: The Art of Changing Your Mind. Penguin Audio.

7. Probability and Risk

1 O’Brien, J., & Audio, P. (2020). How Not to Be Wrong: The Art of Changing Your Mind. Penguin Audio.

2 O’Brien, J., & Audio, P. (2020). How Not to Be Wrong: The Art of Changing Your Mind. Penguin Audio.

3 Goeke, N. (2021, July 12). How Not To Be Wrong Summary. Four Minute Books. Retrieved December 15, 2021, from https://fourminutebooks.com/how-not-to-be-wrong-summary/

4 Mathematics of Risk. (n.d.). Westfield MA. Retrieved December 15, 2021, from https://www.westfield.ma.edu/math/MathWeb/Actuarial/PDFs/342-Intro-to-Risk.pdf

5 Mathematics of Risk. (n.d.). Westfield MA. Retrieved December 15, 2021, from https://www.westfield.ma.edu/math/MathWeb/Actuarial/PDFs/342-Intro-to-Risk.pdf

8. Test Your Mathematical Might

1 Oakley, B. (2014) A mind for numbers: How to excel at math and science (even if you flunked algebra). TarcherPerigee.

2 Oakley, B. (2014) A mind for numbers: How to excel at math and science (even if you flunked algebra). TarcherPerigee.